Вот ссылка на проекты с практической: генерирование напряжения с помощью ШИМ, стабилизация выхода повышающего Step-Up конвертера с помощью пропорционального регулятора:
MCU_Lab4.rar
1. Концепт ШИМ
- как регулировать мощность?
- можно тупо включить резистор (реостат) с нагрузкой -- но тогда на самом регулирующем элементе рассеется много мощности
- еще можно включать и выключать нагрузку, как в микроволновке -- тогда средняя мощность зависит от того на сколько мы включили по сравнению с тем сколько она выключена
- скважность $\alpha$ сигнала прямоугольной формы -- это отношение времени $\tau_1$ в течении которого сигнал равен 1, к периоду импульсов $T$. $\alpha = \tau_1 / T$
- среднее значение сигнала $\bar U$ за время $T$ (чисто математически): $\bar U = \frac{1}{T}\int_0^T u(t) dt$
- среднее значение сигнала для прямоугольного сигнала размахом от 0 В до $U_{max}$ составляет $\bar U = \alpha U_{max}$.
- чтобы сделать из прямоугольного сигнала изменяемой скважности сигнал, близкий к постоянному напряжению -- необходимо пропустить его через фильтр низких частот (ФНЧ)
- средние значения сигналов на выходе и входе фильтра низких частот равны,
- отсюда, пропустив импульсный сигнал через ФНЧ, получаем на его выходе сигнал, близкий к постоянному напряжению в $\alpha U_{max}$ вольт, если частота среза ФНЧ значительно ниже, чем частота следования импульсов $1/T$
-действие ШИМ и сигнал на выходе после фильтра

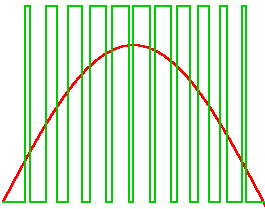
- простейшим фильтром может служить RC-фильтр
с частотой среза $f_c = (2 \pi R C)^{-1}$
- в реальности сигнал на выходе фильтра имеет колебания относительно желаемого генерируемого напряжения

- амплитуду $\Delta$ этих колебаний можно оценить, зная частотную характеристику фильтра $A(f)$ -- зависимость коэффициента усиления от частоты: $\Delta \approx U_{max} A(T^{-1})$ (это взято если аппроксимировать сигнал ШИМ синусоидой частотой $T^{-1}$)
- колебания максимальны по амплитуде при $\alpha = 0.5$
- с другой стороны, фильтр низкой частоты для формирования сглаженного напряжения действует как инерционный элемент: если мы хотим генерировать изменяющийся с некоторой частотой сигнал $f_g$, то, в лучшем случае, на выходе фильтра мы получим сигнал амплитудой $U_{max} A(f_g)$
- т.е. между точностью формирования сигнала и быстродействием существует очевидное противоречие: чем выше точность, тем хуже быстродействие
- на практике выбирают удовлетворение неравенств с запасом $T^{-1} > f_c$, $f_g < f_c$
- ШИМ применяется главным образом также для регулирования токов при управлении двигателями постоянного и переменного напряжения (синхронные и асинхронные) -- частотно-регулируемый электропривод (aka частотники)
- при использовании частотников возможно регулировать частоту вращения вала двигателя от 0 до номинального и увеличить момент до 1.8 от номинального -- т.е. есть возможность исключить применение редуктора
- структура частотника для управления трехфазным двигателем:

- управление однофазным двигателем

- ШИМ применяется для и в усилителях аудиосигналов -- усилители класса D
2. ШИМ в микроконтроллерах
- для генерации ШИМ в микроконтроллерах используется стандартная схема -- как дополнительная опция к таймерам
- таймер TCNT инкрементируется от тактовой частоты и считает от 0 до какого-то значения $N$, например от 0 до 1023, а потом сбрасывается в 0 и так по кругу
- вместе с регистром таймера TCNT используется регистр OCR
- когда таймер сбрасывается в 0 -- то сигнал ШИМ устанавливается в 1, когда значения OCR и TCNT сравниваются -- то сигнал ШИМ устанавливается в 0
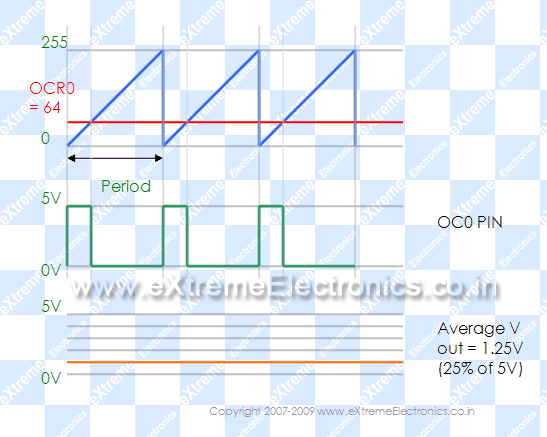
- возможны многие другие режимы генерации ШИМ, отличающиеся изменением значений в регистре TCNT и на выходе ШИМ
3. Концепт управления
- объект управления как статическая функция зависимости выхода от входа $y = f(u)$
- полагаем зависимость $f(u)$ -- прямая, т.е. увеличение $u$ приводит к увеличению $y$ (это очень важное свойство, иначе ничего не работает)
- любая схема управления эксплуатирует инерционные свойства объекта управления
- в реальных объектах управления значения входа и выхода всегда находятся в заданных пределах $u_{min} \le u \le u_{max}$, $y_{min} \le y \le y_{max}$
- микроконтроллер может быть использован для замкнутого управления с обратной связью поскольку имеет АЦП и может генерировать напряжение
- среди двух самых простых способов управления: двухпозиционный регулятор (релейный, ON/OFF, гистерезисный, компаратор), пропорционально-дифференциально-интегральный регулятор (ПИД, PID)
3.1 Релейное управление
- моделируется реле с гистерезисом (как в термостате утюга)
- цель управления: держать выход в пределах от $y_{-}$ до $y_{+}$
- алгоритм: если выход превысил $y_{+}$ -- то выключить $u = u_{min}$, если выход стал меньше $y_{-}$ -- включить $u = u_{max}$
- если границы $y_{-}$ и $y_{+}$ близки -- то происходят переключения с высокой частотой -- схема работает почти как ШИМ
- плюсы: простая реализация, устойчивость, не требует настройки
- минусы: переключения происходят с неодинаковой частотой, часто переключения вообще не желательны, возможно более эффективное управление если плавно изменять вход $u$
3.2 ПИД-регулятор
- два входа: что должно быть $r$ и что на самом деле есть $y$
- система управления пытается скомпенсировать разницу -- получить на
выходе системе такой сигнал, который бы минимизировал бы разницу $r$ и $y$
- если сигнал ошибки положительный $e = r - y$ -- то надо увеличить $y$,
если отрицательный -- то уменьшить $y$
- если увеличение входа $u$ ведет к увеличению выхода $y$, то можно взять
$u = K e$
- это называется пропорциональный регулятор (П-регулятор)
- отображение $f(u)$ может быть нелинейным -- пропорциональный
регулятор способен линеаризовать характеристику системы от $r$ в $y$
- чтобы улучить качество регулирования пропорциональных регуляторов
применяют т.н. пропорционально-интегрально-дифференциальный регулятор (ПИД)
- в ПИД на вход объекта управления подается сигнал из суммы ошибки, ее
производной и интеграла
$u(t) = K_p e(t) + K_i \int e(t) dt + K_d \frac{d e(t)}{dt}$
- дифференциальная компонента $K_d \frac{d e(t)}{dt}$ позволяет уменьшить перерегулирование (превышение выхода на заданным входом)
- интегральная компонента $K_i \int e(t) dt$ позволяет увеличить точность управления и уменьшить воздействие отклоняющих возмущений на выходе
- при реализации на микроконтроллерах интегрирование и дифференцирование производится цифровым способом на основе аппроксимации интеграла и производной конечными разностями
- настройка ПИД-регулятора заключается в выборе коэффициентов усиления $K_p$, $K_i$, $Kd$
- обычно настройка ПИД осуществляется вручную, но ТАУ рассматривает формальные методы, которые реализованы в промышленных регуляторах, имеющих функции автоматической настройки
- при ручной настройке обычно сначала пытаются подобрать только $K_p$, установив остальное в 0, далее подбирают $K_i$ и $Kd$ в зависимости от необходимого поведения системы
- плюсы: высокое качество и плавность регулирования
- минусы: относительная сложность настройки (требуются эксперименты с реальным объектом или его модель) и реализации (необходимо выполнять умножение и цифровое интегрирование и дифференцирование)
Дополнительные материалы:
- чуть более подробно о ШИМ (код на ассемблере не смотреть):
http://easyelectronics.ru/avr-uchebnyj-kurs-ispolzovanie-shim.html
- еще про ШИМ
http://www.pcports.ru/articles/avr3.php
- статья по частотникам (может не самая лучшая, но более полная)
http://www.chipinfo.ru/literature/chipnews/199901/2.html
- ПИД-регулятор на микроконтроллере (аппнота к AVR)
http://www.gaw.ru/html.cgi/txt/app/micros/avr/AVR492.htm
Комментариев нет:
Отправить комментарий