Задание на лабу №2 и пример решения

Следующее задание по лабораторному практикому заключается в том, что вам предлагается выполнить синтез робастного регулятора методом размещения собственных чисел для системы из предыдущей работы.

Задание состоит в следующем:
- синтезировать пропорциональный регулятор по состоянию, который обеспечивает управление без перерегулирования и время реакции на единичный импульс не более 0.5 секунд,
- взять один параметр объекта управления (масса, жесткость, коэффициент демфирования) и в пределах отклонений на 25% от его значения убедиться в робастной устойчивости системы с обратной связью.

Рассмотрим решение на примере из предыдущего задания.



Снова подвижная масса на роликах находится на безмассовой платформе.



После применения законов Ньютона, была получена следующая динамическая система:

$$\dot y = z$$
$$\dot z = - k (y - u) /m$$

Рассмотрим ситуацию, когда масса $m$ изменяется в пределах от 0.75 до 1.25, т.е. актуальная масса записывается в виде $m = m^* + \Delta m$, где $\Delta m \in [-0.25, +0.25]$

Последнее уравнение модели записывается в виде:
$$\dot z = - k (y - u) / (m^* + \Delta m)$$

Следуя этапам синтеза методом размещения полюсов, вычислим предельную вещественную часть собственных чисел:

$$\epsilon = 0.05$$
$$\tau = 0.5$$
$$\lambda_{min} = -\ln(\epsilon)/\tau$$
$$\lambda_{min} = -6$$

Следующий код в MATLAB осуществляет необходимые вычисления:

tau = 0.5;
epsilon = 0.05; 
lambda = -log(epsilon)/tau;

Поскольку данная система -- с одним входом и выходом, то ее описание в пространстве состояний немного модифицируем для упрощения анализа робастности.

$$\begin{pmatrix} \dot y \cr \dot z \end{pmatrix} = \begin{pmatrix} 0 && 1 \cr -k/m && 0 \end{pmatrix} \begin{pmatrix} y \cr z \end{pmatrix} + \begin{pmatrix} 0 \cr k/m \end{pmatrix} u $$

или

$$\dot X = A X + b u$$,
$$Y = C X + d u$$

где
$$A = \begin{pmatrix} 0 && 1 \cr -k/m && 0 \end{pmatrix}$$
$$b = \begin{pmatrix} 0 \cr k/m\end{pmatrix}$$
$$C = \begin{pmatrix} 1 && 0 \cr 0 && 0 \end{pmatrix}$$
$$d = 0 = \begin{pmatrix} 0 \cr 0\end{pmatrix}$$

Такое представление тоже возможно с помощью функции ss в MATLAB. Также мы могли бы оставить прежнее описание с помощью квадратных матриц.

Следующий код описывает систему в пространстве состояний:

m = 1;
k = 1;

A = [0 1; -k/m 0]; 
B = [0; k/m];
C = [1 0; 0 1];
D = [0; 0];

sys = ss(A,B,C,D);

Непосредственно для вычисления коэффициентов усиления обратной связи $K$ используем функцию place, задав предварительно два значения собственных чисел в векторе P:

P = [-lambda -lambda-1];
K = place(A,B,P)

Далее, также в соответствии с этапами проектирования регулятора, получаем матрицу замкнутой системы
$$F = A - B K$$
и выбираем масштабирующий коэффициент по входу $K_{-}$ в соответствии с условием:
$$(A - B K)^{-1} B K_{-} = -I$$
При этом, можно вычислить установившееся состояние системы при $t \to \infty$:
$$X_{ss} = (A - B K)^{-1} B = F^{-1} B$$


Следующий код MATLAB вычисляет масштабирующий коэффициент по входу $K_{-}$ (в коде переменная K_):

F = A - B*K;
x_ss = -inv(F)*B;
K_ = 1/x_ss(1,1);

Далее моделируем замкнутую систему с обратной связью на единичном входном воздействии:

sys = ss(F,B*K_,C,D);
figure
[Y,T] = step(sys);
plot(T, Y(:,1));

И получаем следующую картинку:



Во-первых, ясно видно, что система работает без перерегулирования и действительно обеспечивается единичный сигнал на выходе (в ассимптотике) в ответ на единичный импульс на входе. Однако, заметно, что за время 0.5 секунды сигнал на выходе нарастает только до 0.8 -- быстродействия недостаточно.

Для решения этой проблемы уменьшим собственные числа на 4 и повторим вызов функции place

P = [-lambda-4 -lambda-1-4];
K = place(A,B,P)

В результате получаем приемлимую реакцию:



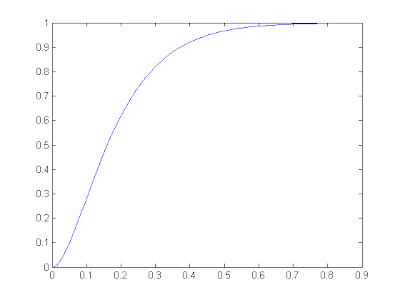
и коэффициенты усиления

K =

  108.8208   20.9829

K_ =

  109.8208

Для решения задачи анализа робастности воспользуемся функциями ureal для создания неопределенной скалярной величины (в данном случае -- массы) и функции uss для создания неопределенной системы в пространстве состояний.

Следующий код в MATLAB описывает неопределенную массу в пределах от 0.75 до 1.25:

dm = 0.25;
m = ureal('m',m,'PlusMinus',[-dm dm]);

Моделирование системы с замкнутой обратной связью выполняется по аналогии с моделированием номинальной системы (без неопределенностей):

A = [0 1; -k/m 0]; 
B = [0; k/m];
C = [1 0; 0 1];
D = [0; 0];

F = A - B*K;

usys = uss(F,B*K_,C,D);
figure
step(usys);

В результате выполнения приведенного кода получаем следующие реакции на выходах:



Видно, что в пределах заданных изменений, система устойчива и обеспечивается регулирование с заданной точностью без перерегулирования.


Аналогичный результат можно было получить в Simulink, модифицировав матрицы коэффициентов усиления обратной связи и масштабирования по входу. Соответствующая модель для Simulink приведена.


Файлы для скачивания
1. Полный скрипт расчета регулятора в MATLAB
2. Модель для Simulink